Modeling Tips

Applying In-Plane Moment to Plates

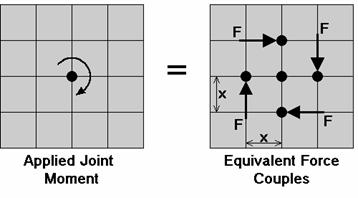
Occasionally you may need to model an applied in-plane moment at a joint connected to plate elements.  The plate/shell element cannot directly model in-plane rotations.  One way around this is to model the in-plane moment as a force couple of in-plane forces.  You would replace the applied in-plane joint moment at 1 joint with 2 or 4 in-plane forces at 2 or 4 joints , which would produce the same magnitude in-plane moment.  See below:

This might require re-meshing the area receiving the moment into smaller plates so that the load area can be more accurately modeled.  If a beam member is attached to the joint and will be used to transfer the moment, than you will want to look at the topic Modeling a Beam Fixed to a Shear Wall below.

Modeling a Beam Fixed to a Shear Wall

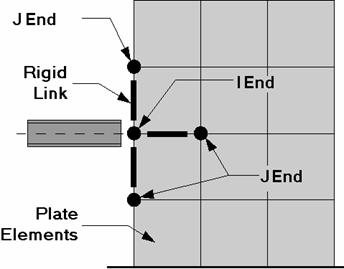
Occasionally you may need to model the situation where you have a beam element that is fixed into a shear wall.  A situation where this may occur would be a concrete beam that was cast integrally with the shear wall or a steel beam that was cast into the shear wall.  The beam cannot just be attached to the joint at the wall because the plate/shell element does not model in-plane rotational stiffness.  A fairly simple work around is to use rigid links to transfer the bending moment from the joint at the wall as shear force to the surrounding joints in the wall.  See Rigid Links in the Modeling Tips section to learn how to create rigid links.  This modeling method provides a more accurate analysis than trying to use a plate/shell element with a “drilling degree of freedom” which attempts to directly model the in-plane rotation.  See the figure below:

The only trick to this method is getting the proper member end releases for the rigid links.  We want to transfer shear forces from the wall joint to the interior wall joints without having the rigid links affect the stiffness of the shear wall.  Notice from the figure that the I-joint for all the links is the joint connected to the beam element, while the J-joints are the ends that extend into the shear wall.  The J-ends of all the rigid links should have their x, Mx, My, and Mz degrees of freedom released.  Only the y and z degrees of freedom (local axes shears) should be connected from the J-ends to the interior wall joints .  This release configuration will allow the shears to be transferred into the wall, but the wall stiffness will not be adversely affected by the presence of the rigid links.

Modeling a Cable

While there is not a true “cable element”, there is a tension only element.  A true cable element will include the effects of axial pre-stress as well as large deflection theory, such that the flexural stiffness of the cable will be a function of the axial force in the cable.  In other words, for a true cable element the axial force will be applied to the deflected shape of the cable instead of being applied to the initial (undeflected) shape.  If you try to model a cable element by just using members with very weak Iyy and Izz properties and then applying a transverse load, you will not get cable action.  What will happen is that the beam elements will deflect enormously with NO increase in axial force.  This is because the change in geometry due to the transverse loading will occur after all the loads are applied, so none of the load will be converted into an axial force.

Guyed Structure (“Straight” Cables)

You can easily model cables that are straight and effectively experience only axial loading.  If the cable is not straight or experiences force other than axial force then see the next section.

When modeling guyed structures you can model the cables with a weightless material so that the transverse cable member deflections are not reported.  If you do this you should place all of the cable self-weight elsewhere on the structure as a point load.  If you do not do this then the cable deflections (other than the axial deflection) will be reported as very large since it is cable action that keeps a guyed cable straight.  If you are interested in the deflection of the cable the calculation is a function of the length and the force and you would have to calculate this by hand.

The section set for the cable should be modeled as a tension only member so that the cable is not allowed to take compression.  See T/C  Members for more on this.

To prestress the cable you can apply a thermal load to create the pre-tension of the cable.  See Prestressing with Thermal Loads to learn how to do this.

Sagging Cables (Large Deflections) & Transverse Loads

One way, (although not an easy one) to model a sagging cable is as follows: First you would define members with the correct area and material properties of the cable.  You should use a value of 1.0 for the Iyy, Izz, and J shape properties.  Next you will want to set the coordinates for your joints at a trial deflected shape for the cable.  Usually you can use just one member in between concentrated joint loads.  If you are trying to model the effects of cable self-weight, you will need to use at least 7 joints to obtain reasonable results.  See the figure below for an example of a cable with 5 concentrated loads:

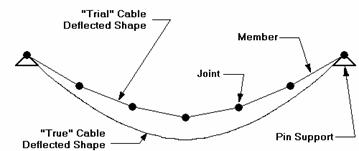
You will want to set the vertical location of each joint at the approximate location of the “final” deflected shape position.  Next you will connect your members to your joints and then assign your boundary conditions.  Do NOT use member end releases on your members.  Make sure you do NOT use point loads, all concentrated loads should be applied as joint loads.  You can model pre-stress in the cable by applying an equivalent thermal load to cause shortening of the cable.

Now you will solve the model with a P-Delta Analysis, and take note of the new vertical deflected locations of the joints.  If the new location is more than a few percent from the original guess, you should move the joint to the midpoint of the trial and new location.  You will need to do this for all your joints.  You will repeat this procedure until the joints end up very close to the original position.  If you are getting a lot of “stretch” in the cable (more than a few percent), you may not be able to accurately model the cable.

Once you are close to converging, a quick way to change all the middle joint coordinates is to use the Block Math operation.  That way you shift many joints up or down by a small amount in one step.

Modeling Inclined Supports

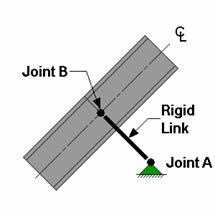
You may model inclined supports by using a short rigid link to span between a joint which is restrained in the global directions and the item to receive the inclined support.  See the figure below:

The rigid link should be “short”, say no more than 0.1 ft.  The member end releases for the rigid link at joint “B” are used to control which degrees of freedom are pinned or fixed in the inclined directions.  This works because the member end releases are in the local member axes.  See Rigid Links in the Modeling Tips section to learn how to create rigid links.

The section forces in the rigid link are the inclined reactions.  Note that you need to make sure the rigid link is connected to the members/plates at the correct inclined angle.  You can control the incline of the angle using the coordinates of joints “A” and “B”.  You can also rotate the rigid link to the proper angle.

Reactions at Joints with Enforced Displacements

The reaction at an enforced displacement can be obtained by inserting a very short (.02' or so) rigid link between the joint with the enforced displacement and any attached members.  The member forces in this rigid link will be the reactions at the joint with the enforced displacement.  It is helpful to align the link to be parallel with one of the global axes, that way the local member forces will be parallel to the global directions unless of course you are modeling inclined supports.  See Rigid Links below to learn how to create rigid links. 

Rigid Links

Rigid links are used to rigidly transfer the forces from one point to another and to also account for any secondary moments that may occur due to moving the force.  This is in contrast to using the tether feature for joints where the forces are shared by 2 joint degrees of freedom (DOF), but any secondary moments are lost when tethering the joints .  Tethered joints actually share common DOF and so do not account for the distances between them.  Rigid links do not have any practical internal deformation, I.e. there is no differential movement between the I-joint and the J-joint .  Rigid links may be used to model situations such as compositebehavior or beams fixed to walls modeled with plate elements.  They are also useful for getting information such as reactions at inclined supports or reactions at joints with enforced displacements.

To Make a Rigid Link

  1. On the General tab of the Materials spreadsheet create a material Label called “LINK”.  Enter “1e6 (ksi)” for the value of E.  Blank out the value for G by going to that field and pressing the space bar.  Double check that the Density is set to zero.  Leave all the other values as their defaults.
  2. On the General tab of the Section Sets spreadsheet create a section set Label called “RIGID” with the “LINK” Material.
  3. Move the cursor to the Shape field and hit your space bar to erase the information in this field.
  4. Set the A,and Iy, Iz and Jvalues to “1e6 (based on units of inches)”.
  5. To make a rigid link, on the Member spreadsheet create a member that references the RIGID section set created above.  You can control which DOF are transferred through the link by using the member end releases.

Note

The weight density should be set to zero in case self-weight is used as a loading condition.  If the material used is not weightless, then any gravity loading would cause the rigid link to add a very large load into your model.  (Gravity load is applied as a distributed load with a magnitude equal to the member area times the weight density).

For models with very stiff elements, like concrete shear walls, the rigid link may not be rigid in comparison.  If you see that the rigid link is deforming, then you may have to increase the stiffness of the link.  The easiest way to do this is to increase the A, Iy, Iz, and J values for the RIGID section set.  Make sure that the combination of E*I or E*A does not exceed 1e17 because 1e20 and 8.33e18 are the internal stiffnesses of the translational and rotational Reaction boundary conditions.  If you make a member too stiff, you may get ghost reactions, which tend to pull load out of the model.  (The total reactions will no longer add up to the applied loads.)

 

Modeling a "Gap" (Expansion Joint) Between Structures

A gap element is a member that mimics the behavior of a gap or expansion joint between adjacent structures.

 

 

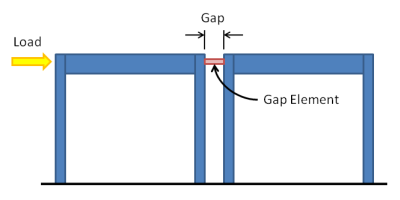
While RISA does not offer the capability to directly create a gap element, one may be indirectly created using the properties of the member and an applied thermal load. The concept is to place a ‘shrunk’ member between adjacent structures. The shrinkage of the member is achieved with a negative thermal load, in the form of a member distributed load.

The amount of shrinkage should be equal to the width of the gap, such that the structures act independently until they move close enough to each other to ‘touch’ and thereby transmit loads to each other. To calculate the thermal load required for a gap use the following formula:

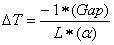
Where:

ΔT = Applied thermal load

Gap = Distance between two structures

L = Length of gap element

α = Coefficient of thermal expansion

 

In order to prevent the gap element from ‘pulling’ its connected structures towards it due to shrinkage it must be defined as a ‘compression only’ member under the advanced options tab. It is also advisable to define the gap element as a rigid material such that the amount of load it transfers once the gap is closed is not affected by elastic shortening.

Lastly, in cases where the applied temperature would need to be of an extraordinary magnitude, it might be useful to increase the coefficient of thermal expansion of the material such that a smaller temperature load would achieve the same shrinkage.